After getting a few great comments on my recent post --- especially regarding using PyPy and Fortran90 to speed up Python --- I decided my simple comparison needed an update.
The big-news is that my tests for this problem actually showed PyPy quite favorably (even a bit faster than the CPython NumPy solution). This is very interesting indeed! I knew PyPy was improving, but this shows it has really come a long way.
Also, I updated the Python-only comparison to not use NumPy arrays at all. It is well-known that NumPy arrays are not very efficient containers for doing element-by-element calculations in Python syntax. There is both more overhead for getting and setting elements than there is for simple lists, and the NumPy scalars that are returned when specific elements of NumPy arrays are selected can be a bit slow when doing scalar math computations on the Python side.
Finally, I included a Fortran 90 example based on the code and comments provided by SymPy author Ondrej Certik. Fortran 77 was part of the original comparison that Prabhu Ramanchandran put together several years ago. Fortran 90 includes some nice constructs for vectorization that make it's update code very similar to the NumPy update solution. Apparently, gfortran can optimize this kind of code very well. In fact, the Fortran 90 solution was the very best of all of the approaches I took (about 4x faster than the NumPy solution and 2x faster than the other compiled approaches).
At Prabhu's suggestion, I made the code available at github under a new GitHub repository in the SciPy project so that others could contribute and provide additional comparisons.
The new results are summarized in the following table which I updated to running on a 150x150 grid with again 8000 iterations.
| Method | Time (sec) | Relative Speed |
|---|---|---|
| Pure Python | 202 | 36.3 |
| NumExpr | 8.04 | 1.45 |
| NumPy | 5.56 | 1 |
| PyPy | 4.71 | 0.85 |
| Weave | 2.42 | 0.44 |
| Cython | 2.21 | 0.40 |
| Looped Fortran | 2.19 | 0.39 |
| Vectorized Fortran | 1.42 | 0.26 |
The code for both the Pure Python and the PyPy solution is laplace2.py. This code uses a list-of-lists for the storage of the values. The same code produces the Pure Python solution and the PyPy solution. The only difference is that one is run with the standard CPython and the other with the PyPy binary. Here is sys.version from the PyPy binary used to obtain these results:
'2.7.1 (b590cf6de419, Apr 30 2011, 03:30:00)\n[PyPy 1.5.0-alpha0 with GCC 4.0.1]'
This is a pretty impressive achievement for the PyPy team. Kudos!
For the other solutions, the code that was executed is located at laplace.py. The Fortran 90 module compiled and made available to Python with f2py is located at _laplace.f90. The single Cython solution is located at _laplace.pyx.
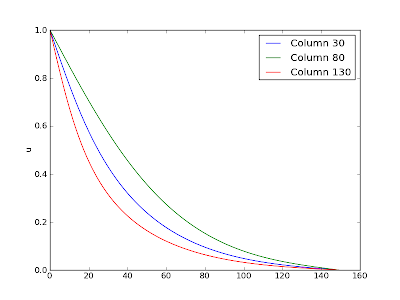
It may be of interest to some to see what the actual calculated potential field looks like. Here is an image of the 150x150 grid after 8000 iterations:
Here is a plot showing three lines from the image (at columns 30, 80, 130 respectively):
It would be interesting to add more results (from IronPython, Jython, pure C++, etc.). Feel free to check out the code from github and experiment. Alternatively, add additional problems to the speed project on SciPy and make more comparisons. It is clear that you can get squeeze that last ounce of speed out of Python by linking to machine code. It also seems clear that there is enough information in the vectorized NumPy expression to be able to produce fast machine code automatically --- even faster than is possible with an explicit loop. The PyPy project shows that generally-available JIT-technology for Python is here and the scientific computing community should grapple with how we will make use of it (and improve upon it). My prediction is that we can look forward to more of that in the coming months and years.

You would get much better performance in PyPy if you've used numpy arrays or array.array instead of list of lists.
ReplyDeleteAlso, for obscure reasons a while loop is a tiny bit faster than a for i in xrange(..) one.
Cheers,
fijal
Does the impressive performance of PyPy suggest that there may be value in a pure Python NumPy? It would run on Iron Python!
ReplyDeleteRichard
Hi Travis. I've been going through a similar test after my EuroPython High Performance Python tutorial, I've written up a v0.1 doc here:
ReplyDeletehttp://ianozsvald.com/2011/06/29/high-performance-python-tutorial-v0-1-from-my-4-hour-tutorial-at-europython-2011/
and v0.2 should be in the works in a couple of weeks. I'll be taking Maciej's advice of trying arrays in PyPy (and hopefully testing the micronumpy lib too). I'm impressed (as you are) with the improvements that the PyPy team are bringing out! The trunk version is even faster than the official v1.5.
Ian.
You should add Cython without numpy.
ReplyDeleteThere is work going on in PyPy to optimize lists of the same type of objects to be as fast as arrays, so you can expect further speed up in the future :)
Thanks for posting the code on github. The PyPy results are amazing. At some level this changes everything.
ReplyDeleteFor what it's worth if I switch this to use array.array("d", [0.0]) * N when creating the arrays it goes about 60% faster on my machine. As Ismael mentioned this will eventually be handled basically automatically.
ReplyDeleteHi Travis, you should also mention, that the loop and vectorized loop are *not* mathematically equivalent, as is shown by printing for example the sum of the values of the array. You would need to greatly increase the number of iterations. Eventually it converges to the same values though, but not for Niter=8000. This was confusing to me, when I was testing the Fortran solution.
ReplyDeleteAnother note is that it seems that the pure Fortran solution is still quite a bit faster than Python + f2py + f90 solution. You might say that the main loop should always be in Python to be fair, but I would argue that since pypy can do some magic (?) optimizations anyway even for the main loop, it makes sense to really see what the maximum speed is. One can just run the laplace_for.f90 example in scipy/speed repository.
If you run laplace_for.f90, make sure you change N to 150, and use for_update2 (vectorized) function in there (for_update1 is default, which is a simple loop). Then I get 0.500s on my computer. For NumPy solution, I get 5.56s, which seems comparable to your timings. As such, doing "pure vectorized Fortran" (0.5s) seems to speed up the "vectorized Fortran" (1.42s) timing almost three times. (f2py fails to compile on my computer due to some missing main() routine, so I can't easily check it myself.)
ReplyDeleteLet me know if someone can reproduce my pure Fortan timing, i.e. being 10x faster than NumPy. So that I don't jump to conclusions too fast.
compiling laplace2.py using 'shedskin -b' gives a speedup of about a 100 times on my PC (http://shedskin.googlecode.com).
ReplyDeleteHi, could anyone include a comparison between Weave and Instant? Thanks!
ReplyDeleteis either of these solution multi-core aware
ReplyDeleteHi, I was wondering why C++/Weave turned out to be so much slower than Fortran in your tests. But there are two major differences:
ReplyDelete* the Weave code uses functions for indexing the array, probably including boundary checks etc.
* the Fortran code is compiled with optimizations
After optimizing the code, Weave beats Fortran on my machine now:
Looped Fortran: 2.050914 seconds
Vectorized Fortran: 1.505481 seconds
Weave: 1.351250 seconds
(Weave: 0.716219 seconds, with openmp)
Some notes:
* This test-bench does not call weave-update before running the actual timing test, which means Weave will be slow when you use it for the first time as it needs to compile and cache the code first. So you have to ignore the first test.
* The multi-core aware solution is easy! (@MySchizuBuddy) Just added a single openmp line and some compiler options and the calculation completed almost 2x faster on my AMD quad core. Change "fno-openmp" to "fopenmp" for testing the openmp solution.
* When changing compiler flags, like "fopenmp", be aware that Weave does NOT recompile the code, as the code-string itself did not change. In order to test different compiler flags, you have to clear your code cache (~/.python27_compiled).
* There is a bug in gcc that prevents vectorization when openmp is enabled http://gcc.gnu.org/bugzilla/show_bug.cgi?id=46032
You will notice this when looking at the verbose gcc output. So once this bug is fixed, one could check out the fully optimized, vectorized, parallelized calculation :D.
And this is the code: http://pastebin.com/MNfhWjSm
Thanks for sharing your info. I really appreciate your efforts and I will be waiting for your further write ups thanks once again.
ReplyDeleteWINDOWS PHONE 7 DEVELOPMENT
I’m usually looking about the internet for content articles that can help me.
ReplyDeleteThank you. It is extremely helpful for me.
would you mind updating your blog with more information?
source: www.wbupdates.com