After getting a few great comments on my recent post --- especially regarding using PyPy and Fortran90 to speed up Python --- I decided my simple comparison needed an update.
The big-news is that my tests for this problem actually showed PyPy quite favorably (even a bit faster than the CPython NumPy solution). This is very interesting indeed! I knew PyPy was improving, but this shows it has really come a long way.
Also, I updated the Python-only comparison to not use NumPy arrays at all. It is well-known that NumPy arrays are not very efficient containers for doing element-by-element calculations in Python syntax. There is both more overhead for getting and setting elements than there is for simple lists, and the NumPy scalars that are returned when specific elements of NumPy arrays are selected can be a bit slow when doing scalar math computations on the Python side.
Finally, I included a Fortran 90 example based on the code and comments provided by SymPy author Ondrej Certik. Fortran 77 was part of the original comparison that Prabhu Ramanchandran put together several years ago. Fortran 90 includes some nice constructs for vectorization that make it's update code very similar to the NumPy update solution. Apparently, gfortran can optimize this kind of code very well. In fact, the Fortran 90 solution was the very best of all of the approaches I took (about 4x faster than the NumPy solution and 2x faster than the other compiled approaches).
At Prabhu's suggestion, I made the code available at github under a new GitHub repository in the SciPy project so that others could contribute and provide additional comparisons.
The new results are summarized in the following table which I updated to running on a 150x150 grid with again 8000 iterations.
| Method | Time (sec) | Relative Speed |
|---|---|---|
| Pure Python | 202 | 36.3 |
| NumExpr | 8.04 | 1.45 |
| NumPy | 5.56 | 1 |
| PyPy | 4.71 | 0.85 |
| Weave | 2.42 | 0.44 |
| Cython | 2.21 | 0.40 |
| Looped Fortran | 2.19 | 0.39 |
| Vectorized Fortran | 1.42 | 0.26 |
The code for both the Pure Python and the PyPy solution is laplace2.py. This code uses a list-of-lists for the storage of the values. The same code produces the Pure Python solution and the PyPy solution. The only difference is that one is run with the standard CPython and the other with the PyPy binary. Here is sys.version from the PyPy binary used to obtain these results:
'2.7.1 (b590cf6de419, Apr 30 2011, 03:30:00)\n[PyPy 1.5.0-alpha0 with GCC 4.0.1]'
This is a pretty impressive achievement for the PyPy team. Kudos!
For the other solutions, the code that was executed is located at laplace.py. The Fortran 90 module compiled and made available to Python with f2py is located at _laplace.f90. The single Cython solution is located at _laplace.pyx.
It may be of interest to some to see what the actual calculated potential field looks like. Here is an image of the 150x150 grid after 8000 iterations:
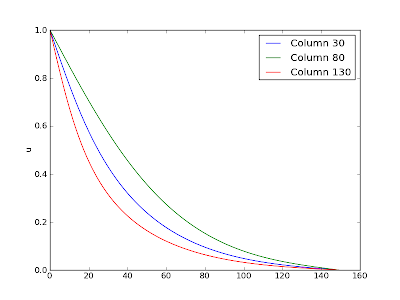
Here is a plot showing three lines from the image (at columns 30, 80, 130 respectively):
It would be interesting to add more results (from IronPython, Jython, pure C++, etc.). Feel free to check out the code from github and experiment. Alternatively, add additional problems to the speed project on SciPy and make more comparisons. It is clear that you can get squeeze that last ounce of speed out of Python by linking to machine code. It also seems clear that there is enough information in the vectorized NumPy expression to be able to produce fast machine code automatically --- even faster than is possible with an explicit loop. The PyPy project shows that generally-available JIT-technology for Python is here and the scientific computing community should grapple with how we will make use of it (and improve upon it). My prediction is that we can look forward to more of that in the coming months and years.